扑克要素练习 发表于 2016-12-13 10:54
这不是很简单吗
3456的面 7或2是必须的 不可能同时有三个人以上拥有
345的面更不用说了 2 或6是必须的
Dracula 发表于 2016-12-13 12:03
采用最优的重叠组合,从原本的15张,提取三张公用牌,从头列到尾还是需要12张,可以组成3个同花顺
但是牌面 ...
Howard 发表于 2016-12-14 03:24
提取三张公用牌,为什么是三张呢?两个同花顺可以共用四张牌,
比如牌面是4567红桃加上一张废牌
JCreeks11 发表于 2016-12-13 15:53
显然A是某一个同花顺的开头,若不然A与定义矛盾。而且有另外一组用到A的同花顺以比A小的牌开头,于是A,A+1 ...
老陈 发表于 2016-12-14 06:38
我认为到目前为止,3楼的论述和“说清楚”离得最近。3楼的论述有个概念“最优重叠组合”,没有说清楚是什么 ...
Dracula 发表于 2016-12-13 16:55
最优组合指的是最大化使用玩家手中的牌组成同花顺也就是2+3=5,因此4张公牌不在考虑序列
老陈 发表于 2016-12-14 07:20
这个貌似还有问题。例如:公牌6789,手中45,这个同花顺应该算56789,不能算45678。 ...
Dracula 发表于 2016-12-13 17:39
我滴老哥,这是反向的逻辑,同花顺是5张的数量不会变
玩家最优2张都使用也没问题!
因此5-2=3,得出的为 ...
Howard 发表于 2016-12-14 06:32
单看此条貌似不成立。
(为了避免A与Ace混淆,我用x代替点数。)
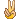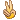
JCreeks11 发表于 2016-12-14 04:13
不好意思,情况太多没想全。现将证明完善如下:
首先排除同花顺里有A2345和AKQJT的情况。假设命题成立。 ...
Howard 发表于 2016-12-14 23:50
这篇可能是最兼具简洁和严密的方式。
由于同花顺的连续性,T2里所有牌要么与T1相交,要么与T3相交,也就 ...
JCreeks11 发表于 2016-12-14 09:56
两同花顺公共的部分不可能是手牌啊,因为手牌不会同时出现在两个同花顺里。
...

snowsnow 发表于 2016-12-15 07:25
如果Ace在高端出现,则A视为14,2视为15,3视为16,4视为17,5视为18,即可被下面证明所涵盖)
----------- ...
Howard 发表于 2016-12-15 07:03
今天传来喜讯,综合整理JCreeks11和老陈(在微信里)的证明过程,采用尽量严谨的方式的简洁证明如下:
( ...
snowsnow 发表于 2016-12-15 18:44
开个玩笑, 同花顺长度为5。
两个同花顺联起来其长度至少为7 (张牌)。
3,4 (5,6,7) 8,9
吹牛无罪 发表于 2016-12-15 01:01
傻瓜版:
用反证法,假设一手牌真的存在3个同花顺。
老陈 发表于 2016-12-15 09:05
公牌不是同花顺,三个人不能同时有同花顺
证明:
老陈 发表于 2016-12-15 23:05
公牌不是同花顺,三个人不能同时有同花顺
证明:
老陈 发表于 2016-12-15 23:05
公牌不是同花顺,三个人不能同时有同花顺
证明:

snowsnow 发表于 2016-12-16 10:25
最简解法 - 图解
1) 任意2个同花顺。两人至少共用1张公共牌, 每人2张手牌 + 3张公共牌。

ceaxyz 发表于 2016-12-17 09:25
1.题目设定了公共牌五张不是同花顺。
2.将公共牌中的同花牌排序,最多五张同一花色牌,则任何同花顺的可能 ...
| 欢迎光临 智游城 (http://zhiyoucheng.co/) | Powered by Discuz! X3.2 |